Interrupted Time Series with post-intervention analysis#

For fixed-period intervention cases (like a marketing promotion, or public policy intervention), we can make our interrupted time series experiment aware of this by providing treatment_end_time as a keyword argument. This splits the post-intervention period into:

  • Intervention period: When treatment is active (from treatment_time to treatment_end_time)

  • Post-intervention period: After treatment ends

This enables analysis of immediate effects, effect persistence, and decay patterns.

Note

For standard two-period ITS analysis (permanent interventions), see Bayesian Interrupted Time Series.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

import causalpy as cp

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
seed = 42

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

Example: Marketing Campaign#

We simulate a 12-week marketing campaign with an immediate effect (+25 units) and partial persistence after it ends (+8 units, ~30% persistence).

# Set up simulation parameters
rng = np.random.default_rng(seed)
n_weeks = 135  # 2 years of weekly data
dates = pd.date_range(start="2022-06-01", end="2024-12-31", freq="W")

# Baseline: trend + seasonality + noise
trend = np.linspace(100, 120, n_weeks)
season = 10 * np.sin(2 * np.pi * np.arange(n_weeks) / 52)  # Annual seasonality
noise = rng.normal(0, 5, n_weeks)
baseline = trend + season + noise

# Add intervention effect
treatment_idx = n_weeks // 2  # Start at midpoint
treatment_end_idx = treatment_idx + 12  # 12 weeks duration

y = baseline.copy()
y[treatment_idx:treatment_end_idx] += 25  # During intervention
y[treatment_end_idx:] += 8  # Post-intervention (persistence)

# Create DataFrame
df = pd.DataFrame(
    {
        "y": y,
        "t": np.arange(n_weeks),
        "month": dates.month,
    },
    index=dates,
)

treatment_time = dates[treatment_idx]
treatment_end_time = dates[treatment_end_idx]

print(f"Treatment starts: {treatment_time}")
print(f"Treatment ends: {treatment_end_time}")
print(f"Intervention period: {treatment_end_idx - treatment_idx} weeks")
print(f"Post-intervention period: {n_weeks - treatment_end_idx} weeks")

Treatment starts: 2023-09-17 00:00:00
Treatment ends: 2023-12-10 00:00:00
Intervention period: 12 weeks
Post-intervention period: 56 weeks

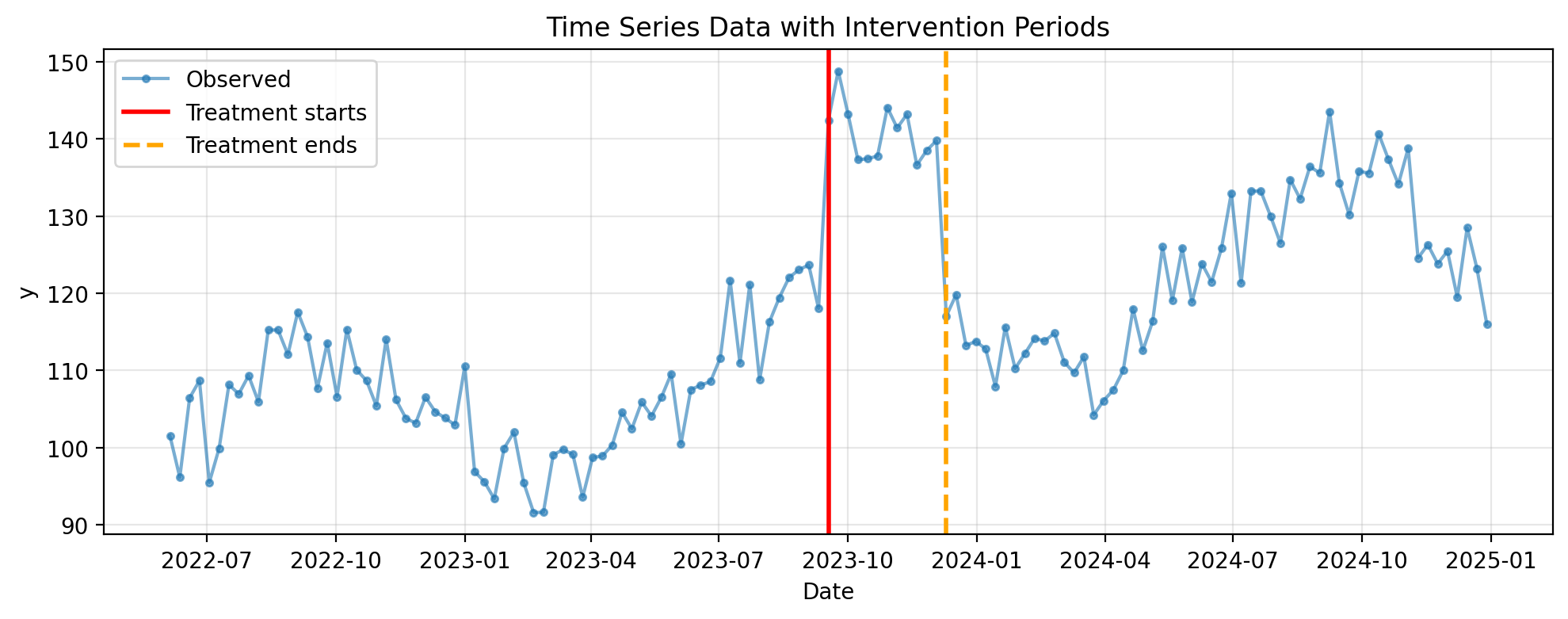
Visualize the Data#

Let’s first visualize the raw time series data to get an intuitive sense of the intervention effect

# Plot the raw data with treatment periods marked
fig, ax = plt.subplots(figsize=(10, 4))

ax.plot(df.index, df["y"], "o-", markersize=3, alpha=0.6, label="Observed")
ax.axvline(
    treatment_time, color="red", linestyle="-", linewidth=2, label="Treatment starts"
)
ax.axvline(
    treatment_end_time,
    color="orange",
    linestyle="--",
    linewidth=2,
    label="Treatment ends",
)

ax.set_xlabel("Date")
ax.set_ylabel("y")
ax.set_title("Time Series Data with Intervention Periods")
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
../_images/6309dc773b3b31c6b8600c8722a8a2bb842b7fbd10a4a0fa1cd7c2266d2b502f.png

Run the Analysis#

Specify treatment_end_time to enable three-period analysis:

result = cp.InterruptedTimeSeries(
    df,
    treatment_time=treatment_time,
    treatment_end_time=treatment_end_time,
    formula="y ~ 1 + t + C(month)",
    model=cp.pymc_models.LinearRegression(
        sample_kwargs={
            "random_seed": seed,
            "progressbar": False,
            "chains": 2,
            "draws": 1000,
        }
    ),
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [beta, y_hat_sigma]
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 37 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]

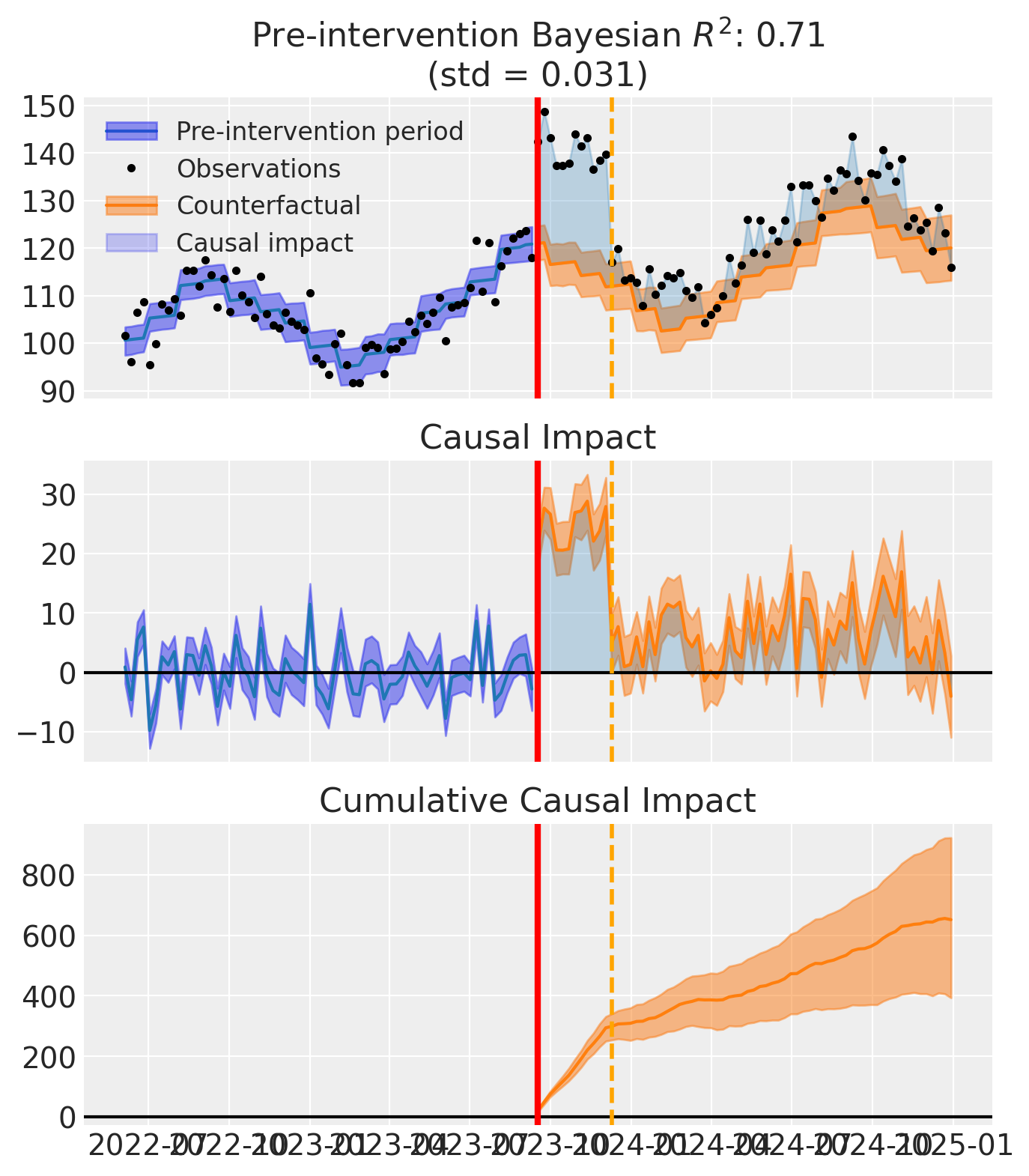
Visualization#

The three-period design visualization adds a vertical line to mark where the treatment ends:

  • Solid red line: treatment_time (intervention start)

  • Dashed orange line: treatment_end_time (intervention end)

The plot shows three panels:

  1. Top panel: Time series with observations, counterfactual predictions, and causal impact shading

  2. Middle panel: Pointwise causal impact over time

  3. Bottom panel: Cumulative causal impact

The vertical line at treatment_end_time clearly separates the intervention period from the post-intervention period, allowing you to visually assess effect persistence and decay.

fig, ax = result.plot()
plt.tight_layout()
plt.show()

C:\Users\jeanv\AppData\Local\Temp\ipykernel_19012\3091047611.py:2: UserWarning: The figure layout has changed to tight
  plt.tight_layout()
../_images/1939b2717a1f39ec95500c0a40a57174ec6b67db889379f137714e2bdd89f0e9.png

Period-Specific Summaries#

Get separate summaries for each period using the period parameter:

# Intervention period
intervention_summary = result.effect_summary(period="intervention")
print(intervention_summary.text)

During intervention (2023-09-17 00:00:00 to 2023-12-03 00:00:00), the average effect was 24.53 (95% HDI [20.86, 27.93]), with a posterior probability of an increase of 1.000. The cumulative effect was 294.37 (95% HDI [250.34, 335.19]); probability of an increase 1.000. Relative to the counterfactual, this equals 21.11% on average (95% HDI [17.38%, 24.73%]).

# Post-intervention period
post_summary = result.effect_summary(period="post")
print(post_summary.text)

Post-intervention (2023-12-10 00:00:00 to 2024-12-29 00:00:00), the average effect was 6.38 (95% HDI [2.32, 10.77]), with a posterior probability of an increase of 0.996. The cumulative effect was 357.26 (95% HDI [129.70, 602.98]); probability of an increase 0.996. Relative to the counterfactual, this equals 5.52% on average (95% HDI [1.70%, 9.40%]).

Comparison Summary#

Use period='comparison' to get a comparative summary showing persistence metrics:

comparison_summary = result.effect_summary(period="comparison")
print(comparison_summary.text)

Effect persistence: The post-intervention effect (6.4, 95% HDI [2.3, 10.8]) was 26.0% of the intervention effect (24.5, 95% HDI [20.9, 27.9]), with a posterior probability of 1.00 that some effect persisted beyond the intervention period.

The comparison summary provides:

  • Post-intervention effect as percentage of intervention effect

  • Posterior probability that some effect persisted

  • HDI interval comparison between periods

Detailed Persistence Analysis#

The analyze_persistence() method automatically prints and returns a detailed summary of effect persistence:

persistence = result.analyze_persistence()

# The method automatically prints results. Access the returned dictionary:
print("\nAccessing results programmatically:")
print(f"  Mean effect during: {persistence['mean_effect_during']:.2f}")
print(f"  Mean effect post: {persistence['mean_effect_post']:.2f}")
print(
    f"  Persistence ratio: {persistence['persistence_ratio']:.3f} ({persistence['persistence_ratio'] * 100:.1f}%)"
)
print(f"  Total effect during: {persistence['total_effect_during']:.2f}")
print(f"  Total effect post: {persistence['total_effect_post']:.2f}")

============================================================
Effect Persistence Analysis
============================================================

During intervention period:
  Mean effect: 24.53
  95% HDI: [20.86, 27.93]
  Total effect: 294.37

Post-intervention period:
  Mean effect: 6.38
  95% HDI: [2.32, 10.77]
  Total effect: 357.26

Persistence ratio: 0.260
  (26.0% of intervention effect persisted)
============================================================

Accessing results programmatically:
  Mean effect during: 24.53
  Mean effect post: 6.38
  Persistence ratio: 0.260 (26.0%)
  Total effect during: 294.37
  Total effect post: 357.26

Summary#

The three-period design enables analysis of temporary interventions:

  • Immediate effects: effect_summary(period="intervention") analyzes effects during the active intervention

  • Persistence: effect_summary(period="post") measures how effects persist after the intervention ends

  • Comparison: effect_summary(period="comparison") provides a comparative summary with persistence metrics

  • Detailed analysis: analyze_persistence() automatically prints and returns a detailed summary with mean effects, persistence ratio (as decimal), and total effects

The persistence ratio (e.g., 0.30 = 30%) indicates how much of the intervention effect “carried over” into the post-intervention period. Note that the ratio can exceed 1.0 if the post-intervention effect is larger than the intervention effect.

In practice, persistence effects could be caused by various mechanisms. For example, in marketing contexts, persistence might reflect brand awareness effects that continue to influence consumer behavior even after the promotional campaign ends.

References#

On this page
Edit on GitHub
Show Source
Consulting and training